[DP] Ch08-3

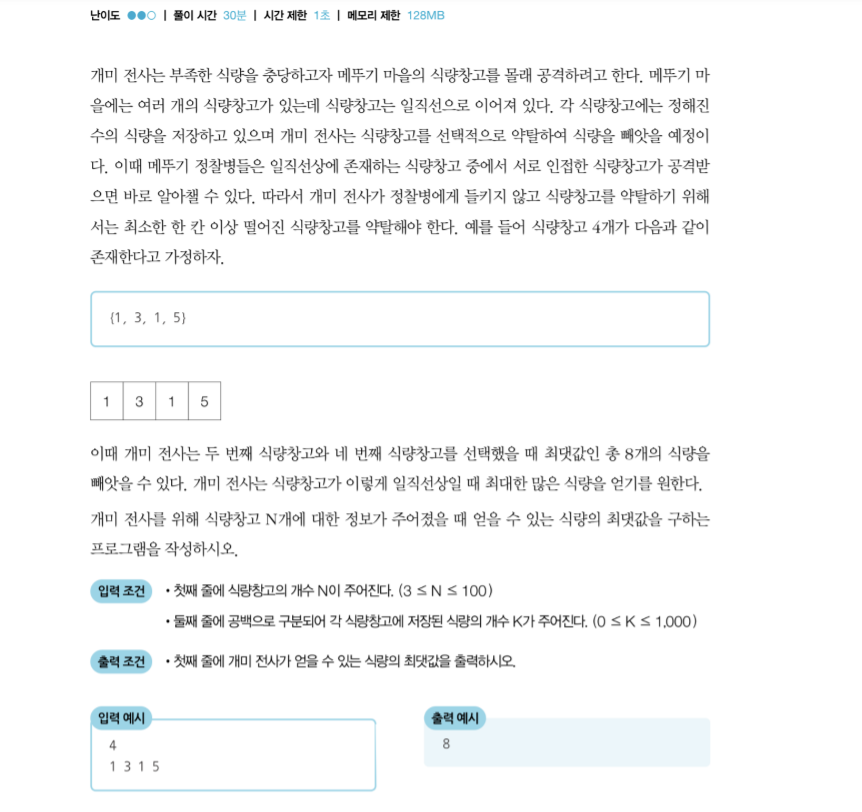
08-3| 개미 전사

🌷 초기 코드:

#include <iostream>
#include <cstdlib>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
	int n;
	vector<int> v(100);
	vector<int> dp(100);
	cin >> n;

	for (int i = 0; i < n; i++) {
		cin >> v[i];
	}
	dp[0] = v[0];
	for (int i = 0; i < n - 3; i++) {
		dp[i] = v[i] + max(v[i + 2], v[i + 3]);
	}
	sort(dp.begin(), dp.end());
	cout << dp[n - 1];

	return 0;
}

🌼 문제풀이 방법:

위의 코드는 맞는 코드는 아니나, 코드다운 코드를 짰다는 점에서 가져왔다. 동적 프로그래밍 문제의 핵심은 점화식 세우기 인 것 같다. 이 문제의 경우도 나름 접근은 비슷하게 했지만, 정확한 점화식을 세우지 못해 문제를 풀지 못했다.

문제를 풀기 위해서는 두 가지만 생각하면 된다. i번째 식량창고에 대해서

1. (i - 1)번째를 털면 i번째를 털지 못한다.
2. (i - 2)번째를 털면 i번째도 털 수 있다.

따라서 v[i - 1]과 v[i - 2]+v[i]중에서 큰 값을 dp 테이블에 저장하면 되는 것이다. i-3번째 이하의 경우는 생각할 필요가 없는데, 한 칸 이상 떨어진 식량창고는 항상 털 수 있기 때문이다.

식을 세우고 나니 문제가 굉장히 간단하게 풀렸다!

🌻 정답 코드:

#include <iostream>
#include <cstdlib>
#include <vector>
#include <list>
#include <string>
#include <set>
#include <algorithm>
using namespace std;

int main() {
	int n;
	vector<int> v(100);
	vector<int> dp(100);
	cin >> n;

	for (int i = 0; i < n; i++) {
		cin >> v[i];
	}
	dp[0] = v[0];
	dp[1] = max(v[0], v[1]); // 둘 중에 큰 값
	// i를 기준으로 할 때,
	// i-1을 털면 i못털고, i-2를 털면 i도 털수 있음
	// 이 두 가지 상황을 비교해서 max를 취함
	for (int i = 2; i < n; i++) {
		dp[i] = max(v[i - 1], v[i - 2] + v[i]);
	}

	cout << dp[n - 1];

	return 0;
}

• BOJ 36
• Algorithm 12
• CodingTest 11
• Web 9
• Javascript 8
• Vue 7
• React 7
• DBProject 4
• Python 3
• Tech-interview 3
• Express 3
• Next 3
• Github 2
• Django 2
• C 1
• C++ 1
• WebGame 1